静岡に暮らす心構えとして知っておきたい地震や火山のこと(その1: 地震の大きさについて)(特任准教授 楠城一嘉)
8月1日 特任准教授 楠城一嘉
富士山や駿河湾をはじめとする自然が豊かで風光明媚な静岡県ですが、この自然は、大陸プレートにフィリピン海プレートがぶつかる地殻変動でできたものです。変動帯の恩恵を享受しつつ、地震や火山のなどによる自然災害に備えるためには、その災害について正しくイメージを持つことが重要です。このコラムでは、不定期ですが、静岡に暮らす心構えとして、知っておきたい地震や火山についてわかりやすく解説します。
今回は、地震の大きさについて成り立つ、かなり普遍的な法則性を説明します。
地震は地下で起きる断層運動で、その大きさはマグニチュード(M)で表します。Mが大きくなると、断層の面積(一般に、断層面は長方形で表し、面積は長さと幅の掛け算で表します)と、すべり量が大きくなります。M9の2011年東北地方太平洋沖地震(以下、東北地震)の断層の長さは400km程度、幅は250km程度で、面積は10万平方キロメートルです。すべり量は場所ごとで違いますが、最大50メートル以上滑ったことが知られています。
2018年6月に起きた大阪府北部を震源とする地震と同程度の大きさのM6地震の場合、長さ・幅は共に数km程度、すべり量は50cm程度、さらに小さいM3の地震の場合、断層長と幅はともに約100m、変位量は約1cmとなります。
断層の長さで見れば、M9とM3の地震では、4,000倍程度違います。もし地震のエネルギーに変換すれば、その違いは約1,000,000,000倍(10億倍)です。
東北地震のようなM9クラスの地震は、日本付近では、現代的な地震観測が始まって以来はじめてであり、地球規模で見ても、M9地震の発生頻度は1世紀の間に平均して1 - 3個程度との見積もりがあります。一方、M3以下の地震は、その地震による揺れが小さいため、我々が気づいていないだけで、毎日日本のどこかで多数発生しています。
これほどまでにスケールが違い、また起こる頻度も桁外れに違う地震現象ですが、横軸にM、縦軸に規模がM以上の地震数Nを対数で取って、地震の規模別の頻度分布を見ると、直線関係が成り立ちます。これは「グーテンベルグ・リヒター則(Gutenberg and Richter law)」と呼ばれています(以下、GR則): Log N = a – bM (aとbは定数)。直線関係の傾きを「b値」と言います。地震の観測条件にもよりますが、一般に、b値は1程度です。b = 1の時、この法則からわかることは、Mが1大きくなると地震数は10分の1になり、Mが2大きくなると100分の1になるということです。
図1(a)は、世界の地震についてNとMの関係を示したものです。b値は1程度でGR則は綺麗に成り立っています。静岡周辺の地震についても、b値は0.8程度とb=1より若干低めですが(図1(b))、法則が成り立っています。
ちなみに、ドイツのグーテンベルグと米国のリヒターが見出したことから、このような法則名になりました。1940年代前半のことです。同様の法則を1930年代後半に日本の地震学者の石本巳四雄と飯田汲事が見出していました。先見の明はありましたが、世界的に浸透した法則名はGR則の様です。
非常に稀な大地震と比較して、頻繁に発生する小さい地震は、一定の法則に従って起きていることが分かりました。これだけスケールの違う現象が、一つの法則で表せるということは、他の自然現象を広く見渡してもあまり無く、GR則は大変一般的な法則として知られています。
この法則が成立する理由は何か、諸説あり未だ決着がついていません。しかし、GR則が成り立つことを仮定して、地下で何が起きているかを理解する研究は、筆者が現在取り組んでいる課題であり(1,2)、次回以降のコラムで解説します。
今回は、地震の大きさについて成り立つ、かなり普遍的な法則性を説明します。
地震は地下で起きる断層運動で、その大きさはマグニチュード(M)で表します。Mが大きくなると、断層の面積(一般に、断層面は長方形で表し、面積は長さと幅の掛け算で表します)と、すべり量が大きくなります。M9の2011年東北地方太平洋沖地震(以下、東北地震)の断層の長さは400km程度、幅は250km程度で、面積は10万平方キロメートルです。すべり量は場所ごとで違いますが、最大50メートル以上滑ったことが知られています。
2018年6月に起きた大阪府北部を震源とする地震と同程度の大きさのM6地震の場合、長さ・幅は共に数km程度、すべり量は50cm程度、さらに小さいM3の地震の場合、断層長と幅はともに約100m、変位量は約1cmとなります。
断層の長さで見れば、M9とM3の地震では、4,000倍程度違います。もし地震のエネルギーに変換すれば、その違いは約1,000,000,000倍(10億倍)です。
東北地震のようなM9クラスの地震は、日本付近では、現代的な地震観測が始まって以来はじめてであり、地球規模で見ても、M9地震の発生頻度は1世紀の間に平均して1 - 3個程度との見積もりがあります。一方、M3以下の地震は、その地震による揺れが小さいため、我々が気づいていないだけで、毎日日本のどこかで多数発生しています。
これほどまでにスケールが違い、また起こる頻度も桁外れに違う地震現象ですが、横軸にM、縦軸に規模がM以上の地震数Nを対数で取って、地震の規模別の頻度分布を見ると、直線関係が成り立ちます。これは「グーテンベルグ・リヒター則(Gutenberg and Richter law)」と呼ばれています(以下、GR則): Log N = a – bM (aとbは定数)。直線関係の傾きを「b値」と言います。地震の観測条件にもよりますが、一般に、b値は1程度です。b = 1の時、この法則からわかることは、Mが1大きくなると地震数は10分の1になり、Mが2大きくなると100分の1になるということです。
図1(a)は、世界の地震についてNとMの関係を示したものです。b値は1程度でGR則は綺麗に成り立っています。静岡周辺の地震についても、b値は0.8程度とb=1より若干低めですが(図1(b))、法則が成り立っています。
ちなみに、ドイツのグーテンベルグと米国のリヒターが見出したことから、このような法則名になりました。1940年代前半のことです。同様の法則を1930年代後半に日本の地震学者の石本巳四雄と飯田汲事が見出していました。先見の明はありましたが、世界的に浸透した法則名はGR則の様です。
非常に稀な大地震と比較して、頻繁に発生する小さい地震は、一定の法則に従って起きていることが分かりました。これだけスケールの違う現象が、一つの法則で表せるということは、他の自然現象を広く見渡してもあまり無く、GR則は大変一般的な法則として知られています。
この法則が成立する理由は何か、諸説あり未だ決着がついていません。しかし、GR則が成り立つことを仮定して、地下で何が起きているかを理解する研究は、筆者が現在取り組んでいる課題であり(1,2)、次回以降のコラムで解説します。
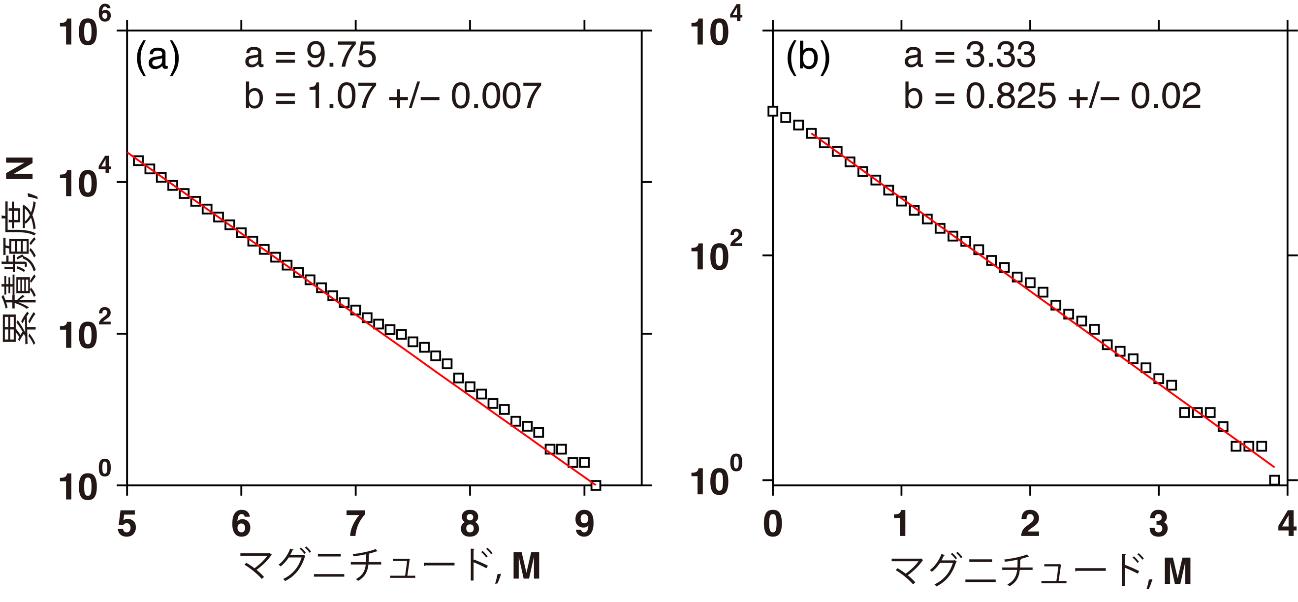
図1. 地震の規模別頻度分布の例。
(a)2000年以降に全世界で発生したM≥5の地震(深さ60kmより浅い)を使用してプロット。GR則を地震のデータにフィットさせた時(赤色の直線)、計算されたbとaの値は記載の通り。
(b)静岡県庁を中心として、半径50kmの円内に起きた地震のうち、2017年の1年間に発生したM≥0の地震(深さ50kmより浅い)についてプトット。
(1)『Nature Communications』掲載論文「南海トラフ巨大地震の震源域における力の状態の推定」
https://www.global-center.jp/review/article/ronbun2018/nankaitorafu/index.html
(2)「10年後の静岡を創るスーパーセミナー(第4回セミナー)」デジタル版 ※県立大学のウェブサイトにつながります。
http://www.u-shizuoka-ken.ac.jp/media/A4-05.pdf(PDF:6.49MB)
https://www.global-center.jp/review/article/ronbun2018/nankaitorafu/index.html
(2)「10年後の静岡を創るスーパーセミナー(第4回セミナー)」デジタル版 ※県立大学のウェブサイトにつながります。
http://www.u-shizuoka-ken.ac.jp/media/A4-05.pdf(PDF:6.49MB)


